Facts about the critical path:
- The critical path is the longest path in the network diagram, or
- The critical path is shortest duration in which the project can be completed.
- Some people like to define the critical path as the path with zero slack (float).In every project (network), there must exist at least one critical path.
- More than one critical path may exist. Multiple paths may share some activities.
- Any critical path must be continuous from the start of the project till its end.
Critical Path Method (CPM) in Project Management
Critical Path Method (CPM), is a project modeling technique developed by Morgan R. Walker and James E. Kelly in late 1950 (Wikipedia).Critical Path
The critical path is the longest path in the network diagram, or
The critical path is shortest duration in which the project can be completed.

Now, review the above diagram.
Did you notice that the path for the first building is biggest in all three? It is thirteen months bigger than the second path, and 18 months bigger than the third path.
This means that if you start working on the first building, you can wait 13 months to start work on the second building, because you can complete second building in 18 months.
Likewise, you will have an 18 month wait time to start working on the third building, because it will take only 13 months to complete. This means that even if you start working on the third building after 18 months from the project start date, you can complete it on time.
This waiting period is known as float or slack.
In ideal conditions, a network diagram should have only one critical path. However, if the network diagram has more than one critical path, you will be in a difficult situation because in this case you will have to manage more than one path in parallel.
As we know, the critical path has the largest duration, and its duration is known as the duration of the project. Since activities on a critical path have no float or slack, no activity can be allowed to be delayed. If this happens, the project will be delayed.
In case of delays, you can use schedule compression tool, such as fast tracking or schedule crashing, to bring the project on track.
Visit: Schedule Compression Techniques – Fast Tracking and Crashing
You must always update the network diagram if there is any change to it so that you can have a better understanding of activities and predict the float, project completion dates, etc.
Benefits of the critical path method
The following are a few benefits of the critical path method:- It shows the graphical view of the project.
- It discovers and makes dependencies visible.
- It helps in project planning, scheduling, and controlling.
- It helps in contingency planning.
- It shows the critical path, and identifies critical activities requiring special attention.
- It helps you assign the float to activities and flexibility to float activities.
- It shows you where you need to take action to bring project back on track.
Limitations/drawbacks of the critical path method
- The critical path method is an optimal planning tool, which always assumes that all resources are available for the project at all time.
- It does not consider resource dependencies.
- There are chances of mis-using float or slack.
- Less attention on non-critical activities, though sometimes they may also become critical activities.
- Projects based on the critical path often fail to be completed within the approved time duration.
Visit: Critical Chain Mehod in Project Management
Procedure for finding the critical path in a network diagram
The following is the procedure to find the critical path on a network diagram:- Draw the network diagram.
- Identify all paths in the network diagram.
- Find the duration of each path.
- The path with the largest duration is the critical path.
Example:
Based on the below network diagram, identify the total paths, critical path, and float for each path.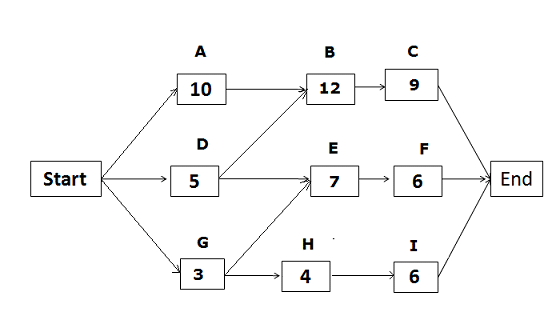
The above network diagram has five paths; the paths and their duration are as follows:
- Start -> A -> B -> C-> End, duration: 31 days.
- Start ->D -> E ->F -> End, duration: 18 days.
- Start -> D -> B -> C -> End, duration: 26 days.
- Start -> G ->H ->I -> End, duration: 13 days.
- Start -> G -> E ->F -> End, duration: 16 days.
The float for the second path “Start ->D -> E ->F -> End” = duration of the critical path – duration of the path “Start ->D -> E ->F -> End”
= 31 – 18 = 13
Hence, the float for the second path is 13 days.
Likewise, we can calculate the float for other paths as well.
Float for the third path = 31 – 26 = 5 days.
Float for the fourth path = 31 – 13 = 18 days.
Float for the fifth path = 31 – 16 = 15 days.
Calculate Early Start (ES), Early Finish (EF), Late Start (LS), and Late Finish (LF)
As we have identified the critical path, and duration of other paths, time to move on more advanced calculations such as Early Start, Early Finish, Late Start, and Late Finish.Calculating Early Start (ES) and Early Finish (EF)
To calculate the Early Start and Early Finish dates, we use forward pass; i.e. we will start from the beginning and proceed to the end.Early Start (ES) for the first activity on any path will be 1, because no activity can be started before the first day of starting the project.
Formula used for calculate Early Start and Early Finish dates.
- Early Start of the activity = Early Finish of predecessor activity + 1
- Early Finish of activity = activity duration + Early Start of activity – 1
Early Start and Early Finish Dates for the path Start -> A -> B -> C -> End
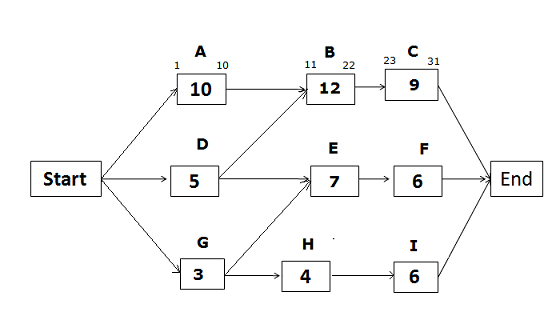
Early Start of activity A = 1 (Since this is the first activity of the path)
Early Finish of activity A = ES of activity A + activity duration – 1
= 1 + 10 – 1 = 10
Early Start of activity B = EF of predecessor activity + 1
= 10 +1 = 11
Early Finish of activity B = ES of activity B + activity duration – 1
= 11 + 12 – 1 = 22
Early Start of activity C = EF of predecessor activity + 1
= 22 +1 = 23
Early Finish of activity C = ES of activity C + activity duration – 1
= 23 + 9 – 1 = 31
Early Start and Early Finish Dates for the path Start -> D -> E -> F -> End
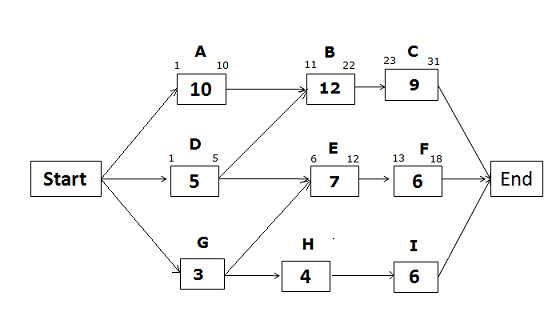
Early Start of activity D = 1 (Since this is the first activity of the path)
Early Finish of activity D = 1 + 5 – 1 = 5
Early Start of activity E = EF of predecessor activity + 1
Now there is a trick. Since the Activity E has two predecessor activities, which one will you select? You will select the activity with the greater Early Finish date. Early Finish of activity D is 5, and Early Finish of activity G is 3 (we will calculate it later).
Therefore, we will select the Early Finish of activity D to find the Early Start of activity E.
Early Start of activity E = EF of predecessor activity + 1
= 5 + 1 = 6
Early Finish of activity E = 6 + 7 – 1 = 12
Early Start of activity F = 12 + 1 = 13
Early Finish of activity F = 13 + 6 -1 = 18
Early Start and Early Finish Dates for the path Start -> G -> H -> I -> End
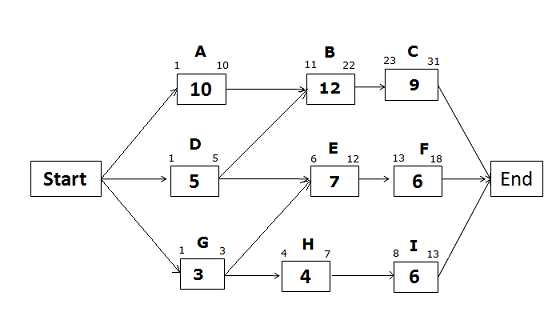
Early Start of activity G = 1 (Since this is the first activity of the path)
Early Finish of activity G = 1 + 3 – 1 = 3
Early Start of activity H = 3 + 1 = 4
Early Finish of activity H = 4 + 4 – 1 = 7
Early Start of activity I = 7 +1 = 8
Early Finish of activity I = 8 + 6 – 1 = 13
Calculating Late Start (LS) and Late Finish (LF)
We have calculated Early Start and Early Finish dates of all activities. Now it is time to calculate the Late Start and Late Finish dates.Late Finish of last activity in any path will be the same as the Last Finish of the last activity on the critical path, because you cannot continue any activity once the project is completed.
Formula used for Late Start and Late Finish dates:
- Late Start of Activity = Late Finish of activity – activity duration + 1
- Late Finish of Activity = Late Start of successor activity – 1
Late Start and Late Finish Dates for the path Start -> A -> B -> C -> End
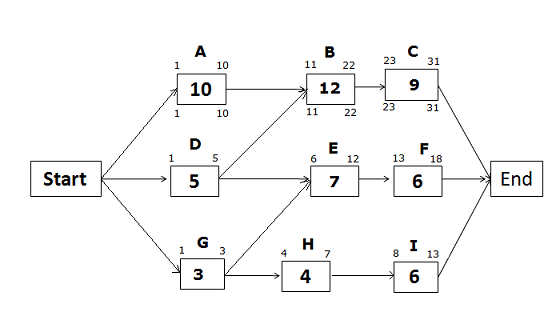
On a critical path, Early Start, and Early Finish dates will be the same as Late Start and Late Finish dates.
Late Start and Late Finish Dates for the path Start -> D -> E -> F -> End
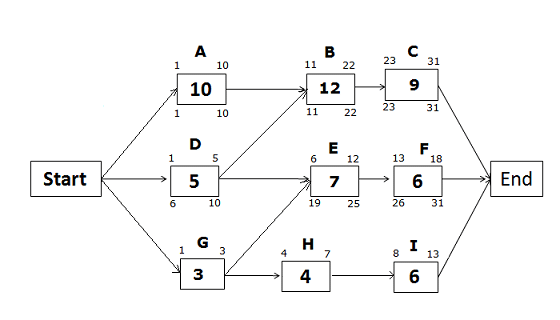
Late Finish of activity F = 31 (because you cannot allow any activity to cross the project completion date)
Late Start of activity F = LF of activity F – activity duration + 1
= 31 – 6 +1 = 26
Late Finish of activity E = LS of successor activity – 1
= LS of activity F – 1
= 26 – 1 = 25
Late Start of Activity E = LF of activity E – activity duration + 1
= 25 – 7 + 1 = 19
Late Finish of activity D = LS of successor activity – 1
If you look at the network diagram, you will notice that activity D has two successor activities, B and E. So, which activity will you select?
You will select the activity with the lower Late Start date. Here, Late Start of activity B is 11, and Late Start of activity E is 19.
Therefore, you will select activity B which has the lower Late Start date.
Hence,
Late Finish of activity D = LS of activity B – 1
= 11 – 1 = 10
Late Start of Activity D = LF of activity D – activity duration + 1
= 10 – 5 + 1 = 6
Late Start and Late Finish Dates for the path Start -> G -> H -> I -> End
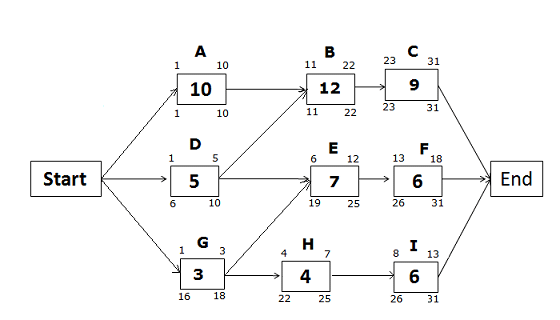
Late Finish of activity I = 31 (because you cannot allow any activity to cross the project completion date)
Late Start of activity I = 31 – 6 + 1 = 26
Late Finish of activity H = 26 – 1 = 25
Late Start of activity H = 25 – 4 + 1 = 22
Late Finish of Activity G = 19 – 1= 18 (we will choose the late start of activity E not activity H, because the Late Start of activity E is lower than the Late Start of activity H)
Late Start of activity G = 18 – 3 + 1
= 16
Calculate the Free Float
I have already written a detailed blog post explaining the total float and free float, therefore, I’m not going to describe it now; rather, I will directly show you its calculation.I strongly recommend you read my blog post on total float and free float to get a better understanding.
Visit: Total Float and Free Float
Formula for the Free Float:
- Free Float = ES of next activity – EF of current activity – 1
Free Float for activity D = ES of activity B – EF of activity D – 1
= 11 – 5 – 1
= 5
Free Float of activity G = ES of E – EF of G – 1
= 6 – 3 – 1
= 2
Here is where this blog post completes. I hope you have enjoyed reading it.